1.枚举(穷举)
将问题的可能解依次列举出来,然后一一带入问题检验,从而从一系列可能解中获得能够解决问题的精确解。需要注意可能解和候选解的筛选条件,可能解之间的影响、代价、穷举的方式。
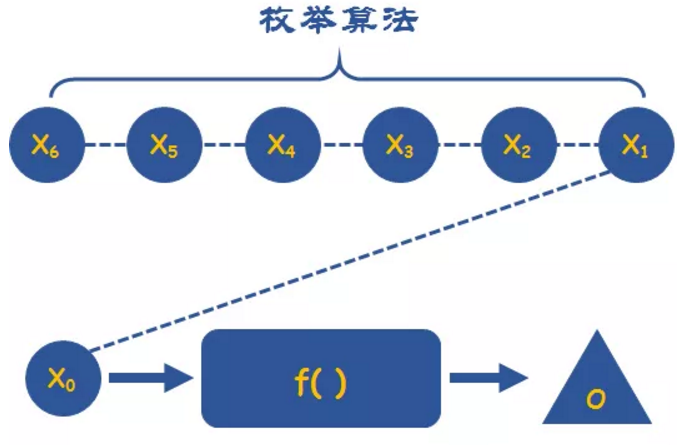
案例:百钱百鸡
公鸡一个五块钱,母鸡一个三块钱,小鸡三个一块钱,现在要用一百块钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?
public class Demo1 {
public static void main(String[] args) {
for (int i = 0; i <= 20; i++) {
for (int j = 0; j <= 33; j++) {
int n = 100 - i - j;
if (i * 5 + j * 3 + n / 3 == 100 && n%3==0) {
System.out.println("公鸡:" + i + "," + "母鸡:" + i + "," + "小鸡:" + (100 - i - j));
}
}
}
}
}2.递推
从已知条件出发,逐步推算出问题的解。计算机在运用递推思想时,大多都是重复性的推理。
每一次推导的结果可以作为下一次推导的的开始,这似乎跟迭代、递归的思想有点类似,不过递推的范畴要更广一些。
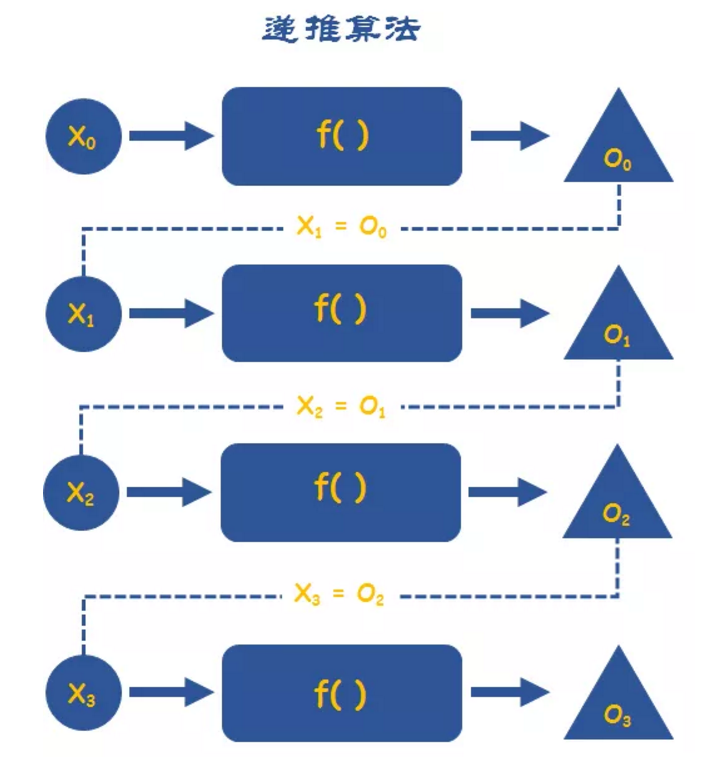
案例:兔子问题
问题:有一只兔子,从第3个月开始每月生1只兔子,小兔子长到第3个月开始每个月也会生1只兔子,假如兔子都不死,问每个月的兔子总数是多少?
public class Demo2 {
//输出10个月,每个月兔子的总数
public static void main(String[] args) {
int nums = 0;
int one_month = 1,two_month = 1;;
for (int month = 1; month <= 10; month++) {
if (month < 3) {
nums = 1;
} else {
//本月兔子数等于前面几个月兔子数的和
nums = one_month+two_month;
one_month = two_month;
two_month = nums;
}
System.out.println("第" + month + "个月" + nums + "只兔子");
}
}
//递归实现
public int rabbit(int month){
if(month<3){
return 1;
}else{
return rabbit(month-1)+rabbit(month-2);
}
}
}Click here to view the copyright notice of this site(点击此处查看本站版权声明)

必须 注册 为本站用户, 登录 后才可以发表评论!