BigDecimal是什么
BigDecimal:位于java.math包下的对超过16为有效位进行精确运算的类,算术运算要通过方法进行操作。
float和double:只能用来做科学计算和工程计算,处理小数时存在精度缺失。
为什么使用BigDecimal?什么时候使用?
//测试浮点数精度缺失
@Test
void contextLoads() {
System.out.println("0.2 + 0.1 = " + (0.2 + 0.1));
System.out.println("0.3 - 0.1 = " + (0.3 - 0.1));
System.out.println("0.2 * 0.1 = " + (0.2 * 0.1));
System.out.println("0.3 / 0.2 = " + (0.3 / 0.1));
}
控制台输出如下:
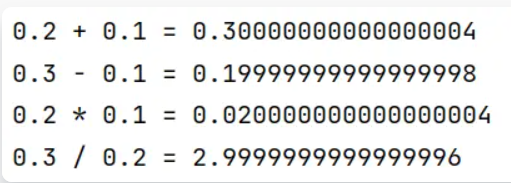
- 如上图,浮点数处理时可能会发生精度缺失。当处理金额相关的数字时,一点点精度缺失当数量级大的时候就是很大损失。
- 浮点数为什么会发生精度缺失呢?
因为float和double都是浮点数,而计算机是二进制的,浮点数会失去一定的精确度。
注:根本原因是:十进制值通常没有完全相同的二进制表示形式;十进制数的二进制表示形式可能不精确,只能无限接近于那个值
- 什么时候使用BigDecimal?
BigDecimal需要慎重使用!虽然BigDecimal解决了浮点数精度问题,但BigDecimal基本上每步运算都需要创建新的BigDecimal对象,比float和double更加的损耗性能。当处理比较重要和对精度有要求的数据(金额)时使用BigDecimal。
BigDecimal怎么使用?
1.创建BigDecimal对象
- BigDecimal(int) 创建一个具有参数所指定整数值的对象
- BigDecimal(double) 创建一个具有参数所指定双精度值的对象(不推荐使用)
- BigDecimal(long) 创建一个具有参数所指定长整数值的对象
- BigDecimal(String) 创建一个具有参数所指定以字符串表示的数值的对象(推荐使用)
不推荐将浮点数作为形参传入构造函数
//测试浮点数当做形参传入构造函数时精度缺失
@Test
void contextLoads() {
BigDecimal bigDecimal = new BigDecimal(0.1);
System.out.println("bigDecimal值为: " + bigDecimal);
/**
控制台输出:bigDecimal值为: 0.1000000000000000055511151231257827021181583404541015625
*/
如上代码结果所示: 参数类型为double的构造方法的结果有一定的不可预知性。new BigDecimal(0.1)它实际上等于0.1000000000000000055511151231257827021181583404541015625。
这是因为0.1无法准确地表示为 double(或者说对于该情况,不能表示为任何有限长度的二进制小数)。这样,传入到构造方法的值不会正好等于 0.1(虽然表面上等于该值)。
推荐使用字符串为形参传入构造函数
(1)String类型参的构造方法是完全可预知的。比如 new BigDecimal(“0.1”) 将创建一个 BigDecimal对象,它正好等于预期的 0.1。因此,比较而言,通常建议优先使用String构造方法。
(2)当是形参为浮点数时,推荐先将浮点数转换为字符串类型然后放入构造函数中。例如:new BigDecimal(Double.toString(value))或者new BigDecimal(new Double(value).toString())。代码如下图所示:
@Test
void contextLoads() {
BigDecimal bigDecimal = new BigDecimal(Double.toString(2.1));
BigDecimal bigDecimal1 = new BigDecimal(new Double(2.1).toString());
System.out.println("bigDecimal值为: " + bigDecimal);
System.out.println("bigDecimal1值为: " + bigDecimal1);
}
/**
*控制台输出:
*bigDecimal值为: 2.1
*bigDecimal1值为: 2.1
*/
2.调用方法进行运算
四则运算:
- add(BigDecimal) BigDecimal对象中的值相加
- subtract(BigDecimal) BigDecimal对象中的值相减
- multiply(BigDecimal) BigDecimal对象中的值相乘
- divide(BigDecimal) BigDecimal对象中的值相除
BigDecimal类型转换为其它类型:
- toString() 将BigDecimal对象的数值转换成字符串。
- doubleValue() 将BigDecimal对象中的值以双精度数返回。
- floatValue() 将BigDecimal对象中的值以单精度数返回。
- longValue() 将BigDecimal对象中的值以长整数返回。
- intValue() 将BigDecimal对象中的值以整数返回。
BigDecimal大小比较:
int returnValue = bigDecimal1.compareTo(bigDemical2)
两个BigDecimal对象进行大小比较,
- 当returnValue = -1,表示bigdemical小于bigdemical2;
- 当returnValue = 0,表示bigdemical等于bigdemical2;
- 当returnValue = 1,表示bigdemical大于bigdemical2;
注: 除法(divide)运算的时候,结果不能整除而有余数时会报java.lang.ArithmeticException错误:
为了避免此错误产生,在进行除法运算的时候,针对可能出现的小数产生的计算,可以在divide方法中多传两个参数 divide(BigDecimal divisor, int scale, RoundingMode roundingMode) 也就是divide(new BigDecimal(value),保留小数点后几位小数,舍入模式)。如下图代码所示:
//测试除法有余数时使用divide(BigDecimal divisor, int scale, RoundingMode roundingMode)
@Test
void Test() {
BigDecimal divisor = new BigDecimal(10);//除数
BigDecimal dividend = new BigDecimal(3);//被除数
System.out.println(divisor.divide(dividend,2,BigDecimal.ROUND_CEILING));// 输出10/3
}
/**
*控制台输出:3.34
*/
舍入模式
// Rounding Modes //向远离0的方向舍入 public final static int ROUND_UP = 0; //向零方向舍入 public final static int ROUND_DOWN = 1; //向正无穷方向舍入 public final static int ROUND_CEILING = 2; //向负无穷方向舍入 public final static int ROUND_FLOOR = 3; //向(距离)最近的一边舍入,除非两边(的距离)是相等,如果是这样,向上舍入, 1.55保留一位小数结果为1.6,也就是我们常说的“四舍五入” public final static int ROUND_HALF_UP = 4; //向(距离)最近的一边舍入,除非两边(的距离)是相等,如果是这样,向下舍入, 例如1.55 保留一位小数结果为1.5 public final static int ROUND_HALF_DOWN = 5; //向(距离)最近的一边舍入,除非两边(的距离)是相等,如果是这样,如果保留位数是奇数,使用ROUND_HALF_UP,如果是偶数,使用ROUND_HALF_DOWN public final static int ROUND_HALF_EVEN = 6; //计算结果是精确的,不需要舍入模式 public final static int ROUND_UNNECESSARY = 7;
BigDecimal总结
(1) BigDecimal基本上每步运算都需要创建新的BigDecimal对象,比float和double更加的损耗性能。当处理比较重要和对精度有要求的数据(金额)时使用BigDecimal。
(2)不推荐将浮点数作为形参传入构造函数,推荐使用字符串为形参传入构造函数。
(3)当调用divide(除法)时,为了避免此java.lang.ArithmeticException错误产生,可以调用 divide(BigDecimal divisor, int scale, RoundingMode roundingMode) 也就是divide(new BigDecimal(value),保留小数点后几位小数,舍入模式)方法。
Click here to view the copyright notice of this site(点击此处查看本站版权声明)

必须 注册 为本站用户, 登录 后才可以发表评论!